Kodjo Kudiabor †
Primzahlen sind nach dem Aufbauprinzip des Atom-Periodensystems organisiert 14. 06.2003
Erklärung | Kontakt | zurück
nS1={ 1,3,11,15,37.55,87} p1= { 2,3,5,7,11 13, 17...}
Die natürliche Folge von den Ordnungszahlen der nS1-Atome sowie von den Primzahlen p1
treten unregelmäßig auf. Der Grund für die scheinbare Unregelmäßigkeit
der nS1-Atrome ist bekannt:
Sie gehören zu Gruppe 1A des Atom-Periodensystems, wo sie als führende Elemente der
Perioden K,L,M,N,O,P,Q ( der 7 Hauptquantenzahlen) auftreten. Eine Analyse der kanonischen
Primzahlzerlegung - N=pm x p1a x p2b x p3c x. mit .(. p < p1 < p2 < p3..... alle Primzahlen
) - zeigt:. Primzahlen sind ähnlich wie Gruppe 1A organisiert und besitzen auch analoge
Charakteristika .
DAS ANALOGON: Tafel A unten zeigt die 7 Hauptquantenzahlen. Der Anfang jeder n-Quantenzahl
ist von einem Element der nS1-Atome (Wasserstoff und Alkalimetalle) besetzt. In Tafel B besetzen
die ersten beiden Primzahlen 2,3 die Anfangspositionen der ersten beiden Primperioden folgender
Gestalt: 1.-Primperiode: N={ 2x1, 2x3, 2x5, 2x7, 2x32, 2x11, } Eine Primperiode entsteht aus
der Gruppe natürlicher Zahlen, deren kanonischen Primfaktoren eine gemeinsame kleinste
Primzahl (in diesem Beispiel die Zahl 2 ) enthalten. So ist auch die Zahl 123450 = 21 x 31
x 52 x 8231 =21 x 61 725 eine Element der 21 x 1-Primperiodebahn,. wie später genauer
zu zeigen ist.

Die 1. und 2. Primperioden (oben) erkennt man als 1. und 2. Parallelbahnen im Prim- Periodendreieck
(s. unten) wieder. Die Bahn-Elemente sind äquidistant geordnet.. Die Balkenlänge
(farbig dargestellt) deutet auf die Äquidistanten Intervalle hin: d=4 und .d=6 bei der
1. bzw. 2, Periodenbahn.. Die Hypotenuse verbindet die Anfangspositionen aller Parallelbahnen
in der Gestalt von führenden Bahnelementen: p1={ 21x 1; 31 x 1; 51 x 1; 71 x 1...}, die
die Einzelprimzahlen (pm= p1 ; m=1) in ihrer natürlichen (aber als unregelmäßig
bekannten) Reihenfolge : p1={2,3,5,7,11, 13,1 7,19..}.widerspiegelt. Die Dreieckfläche
erfasst alle zusammengesetzten Zahlen. Auf der 1. Primperiodenbahn betrachtet, erscheinen zusammengesetzten
Bahnelemente in dieser Reihenfolge: z={21x 3; 21x 5; 21x 7; 21x 1; 21x 9....}. Die Horizontale
durch die Dreieckspitze ist die Übertragachse für Exponentialprimzahlen pm (m>1).
Sie treten in folgender Form auf: pm ={22, 23, 32, 24, 52, 33,25, 72, 26, 34...}. die variable
Grundzahlen aufweisen, anders als die Dezimal- Übertragachse: Dn = {100, 101 102, 103,.....}
Ähnlich wie Gruppe 1A. welche die ns1–Atome, also die führenden Elemente der
Perioden K,L,M,N,O,P;Q des Atom-Periodensystems zusammenfasst, stellen wie fest, dass die Hypotenuse
die führenden Bahnelemente p1={ 21x 1; 31 x 1; 51 x 1; 71 x 1...},des Prim-Periodendreiecks
verbindet.
DAS DREIECK-PERIODENSYSTEM VON PRIMZAHLEN
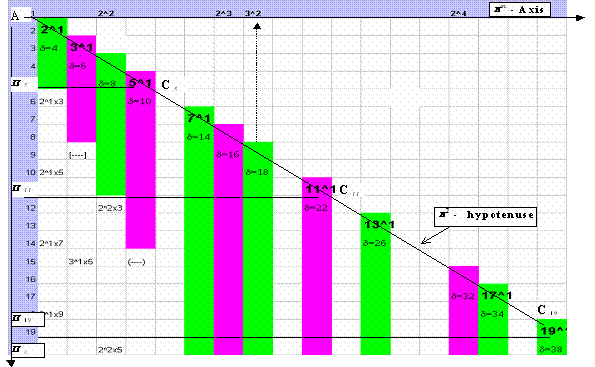
DAS pm- GESETZ DES PRIM-PERIODENDREIECKS: N=pm(2n+1)
Die Darstellung kanonischer Primfaktoren N=pm x p1a x p2b x p3c x. mit .(. p < p1 < p2
< p3..... alle Primzahlen ) für alle natürlichen Zahlen N={1,2,3,4,5..,,n+1..}
lässt sich in die Form N= pm x q, mit q=2n+1 transformieren. Wie aus der Falluntersuchung
Tafel C unten hervorgeht, ist q stets ein Element der natürlichen ungeraden Zahlenfolge:
q={1,3,5,7,9,11,13,l5...} BEISPIEL: 123450 = 21 x 31 x 52 x 8231 =21 x 61 725. Allgemein gilt:
Ist eine Primzahl bekannt, z.B. die Mersenne Primzahl, Mp=25-1=311, dann lassen sich einfach
durch Multiplikation von 311 mit laufenden ungeraden Zahlen, alle Elemente auf der 311-Periodenbahn
ermitteln: N=311 x (2n+1). Mit q1=1 ist n1=0; qx=123 ist nx=61. Daraus erhält man die
entsprechenden Elemente : N1= 31, Nx=1891.Beide gehören zu der 311 –Primperiodebahn.
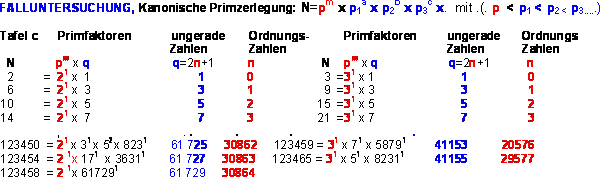
DIE NULL-ORDNUNGSZAHL Der Parameter n in q= (2n+1) gibt die Position (d.h. Ordnungszahl ) der
Elemente N auf einer ins Auge gefassten Prim-Periodenbahn an: n={0,1,2,3,4,5...}.. Der Null-Ordnungszahl
(n=0) kommt eine besondere Bedeutung zu: Sie ist die Anfangsposition der Bahn und liegt immer
auf der Hypotenuse, die Spur aller Einzelprimzahlen: N=311 x (2n+1) =311 x 1, n=0.
Wir sehen einen weiteren Aspekt der der Ähnlichkeit: Im Prim-Periodendreieck weist die
Hypotenuse auf Primzahlen p1= { 2,3,5,7,11 13, 17...} mit Null-Ordnungszahlen hin. Im Atom-Periodensystem
deutet Gruppe 1A ihrerseits auf nS1-Atome nS1={ 1,3,11,15,37.55,87} mit Null-Nebenquantenzahlen
(bzw. Null-Energieniveaus. Tafel D) hin . Die beiden unregelmäßigen Zahlenfolgen,
betrachtet in den Perioden-Strukturen ihres ähnlichen Aufbauprinzips, sind natürlich
und regelmäßig..

DIE 4 SEKTOREN DES DREIECK-PERIODENDREIECKS:
Die Vertikale des Dreiecks (s.oben) stellt die Achse aller natürlichen Zahlen N dar. Ihre
Primfaktoren in der transformierten Form N= pm (2n+1) verteilen sich nach folgenden Bedingungen
in 4 Sektoren:

DIE DEFINITION DER EINZELPRIMZAHL: Die Transformation der kanonischen Primfaktoren N= pm (2n+1)
definiert eindeutig eine Einzelprimzahl, wenn der Exponent den Wert m=1 und die Ordnungszahl
n=0 annehmen. In der Dreieck-Graphik ist die Hypotenuse die Spur aller Null-Ordnungszahlen..
Bitte beachten: In der zahlenmäßiger Ausrechnung der Einzelprimzahl N= 311 (2n+1)
= 311x 1; n=0, ist der Faktor 1 zulässig und sogar Vorschrift, da er auf die Null-Ordnungszahl
der Einzelprimzahl hinweist. Insbesondere ist die Schreibweise 3i1x 1 keine zusammengesetzte
Zahl; diese ist nur bei Exponent m>0 und bei den Ordnungszahlen n=[---,1,2,3,4,5...} eindeutig
definiert: Nz= 311 (2n+1)= 311 x 3; n=1
DIE DEFINITION DER EXPONENTIAL-PRIMZAHL: pm ist durch die Bedingungen m>1 und n=0 in N=
pm (2n+1) eindeutig bestimmt. De Horizontale durch die Dreieck-Spitze stellt die Übertragachse
höherer Ordnung dar, die die Exponential-Primzahlen in der Folge :pm={22, 23, 32, 24,
52, 33, 25, 72..}. aufnimmt. Ihre Funktion ist vergleichbar mit der Übertragachse des
Dezimalsystems: Dm=[1..9,101; 91..99,102, 991..999,103.}. mit dem Unterschied, dass die Grundzahl
10 im Dezimalsystem konstant ist.
DIE DEFINITION DER ZUSAMMENGESETZTEN ZAHL: Hier gelten: m>0 und n>0 in N= pm (2n+1).
Alle zusammengesetzten Zahlen (z.B.: p=2, m=1, n=1 ; N=21 x 3 ) sind innerhalb der Dreieck-Fläche
des Prim-Periodensystems eingebettet.
DIE ZAHL 1: Sie entsteht, wenn m=0 und n=0 in N= pm (2n+1). In der Grafik ist p0 =1 der Schnittpunkt
von den 3 anderen Sektoren: p1-Hyponuse, pm- Übertragachse und von der Spitze der Dreieckfläche,
innerhalb welcher die zusammengesetzten Zahlen befinden. Warum ist die Zahl 1 keine Primzahl
ist ? lautet die 2. Kardinalfrage der Primzahlen unter einer unzufriedenen Gruppe von Mathematikern.
Die Ursache ist der Sonderstatus eines Schnittpunktes von 3 verschiedenen Eigenschaften, was
kein einzigartiges Phänomen in der Natur darstellt. Die Zahl 1 p0 =1 an der Spitze des
Dreiecks ist der eutektische Punkt der natürlichen Zahlenstruktur ähnlich wie bei
Zustandsdiagrammen verschiedener Atome einer Legierung, die sich am gemeinsamen tiefsten Schmelzpunkt
Eutektikum schneiden. http://www.ul.ie/~walshem/fyp/Eutectic%20alloys.htm
GLEICHUNG DER POPULATIONSVERTEILUNG AUF DER PRIM-PERIODENBAHN: d=2pm
Das Intervall d zwischen benachbarten Elementen ist äquidistant für Elemente auf
gleicher Prim-Periodenbahn. Für unterschiedliche Bahnen jedoch wächst d exponentiell:
d=2pm;. BEISPIEL

Die Periodenbahn mit der kleinsten Primzahl, 21(2n+1) besitzt das kleinste äquidistante
Intervall d=4 und damit die größte Population von Bahnelementen im gesamten natürlichen
Zahlensystem. Das
bedeutet auch: Jede 4. natürliche Zahl ist ein Element des 2^1-Periode. .Auf der nächst
höheren 3^1- Periode mit d=6, ist es jede 6. natürliche Zahl, Das entspricht also
einem Häufigkeitsverhältnis von 1:6. Die entsprechenden schwindenden Werte für
die größer werdenden Primzahlen Ma und Mb (10-stellig) sind 1: 2 x 31 bzw. 1: 2
x 2 147 483 647. Bei der 4-Millionen-stellige Primzahl M39 ist die Häufigkeit nur noch
1: 2 X 213 446 917-1. Also unter jedem Haufen von 8-millionen natürlichen Zahlen existiert
nur eine einzige Zahl, in welcher M39 als der kleinste Prim-Faktor vorkommt. Und die findet
man nur auf der M39-Prim-Periodenbahn, wo die Einzelprimzahl M39= (213 446 917-1) x (2n+1)
mit der Null-Ordnungszahl (n=0) auf der Prim-Hypotenuse auftritt. M39 ist die bisher größte
bekannte Mersenne Primzahl. http://www.mersenne.org
Damit sind wir bei der 3. Kardinalfrage der Primzahlen gelandet: Warum sind größer
werdende Riesen-Primzahlen spärlich verteilt ? Offenkundig ist das äquidistante Intervall
d=2pm dafür verantwortlich, welches sich mit wachender Primzahl pm exponentiell erweitert.
Die exakte Verteilungsfrequenz f betragt f =1/d. wie Tafel E) unten prozentuell zeigt. (Verglich::
Frequenz- Näherungsformel aus dem Primzahlsatz, p(n) ~ n/(ln(n)): f ~ 1/ln(x),): http://hades.ph.tn.tudelft.nl/Internal/PHServices/Documentation/MathWorld/math/math/p/p594.htm
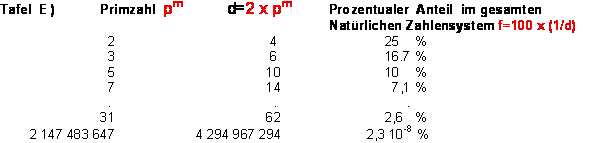
In der Kryptography, wo extrem große Primzahlen als elektronischer Verschlüsselungscode
von Nachrichten und Unterschriften zur Anwendung kommen, sagt Tafel E) im Prinzip aus, dass
die Frequenz f=2,3 10-8 % eine höhere Sicherheit bietet als etwa f =2,6 % . Beispiel einer
kryptographischen .Zahl bestehend aus 2 großen Primzahlen ist: RSA-2048 mit 2048 bits
äquivalent zu 617 Dezimalstellen:.
http://www.rsasecurity.com/rsalabs/challenges/factoring/numbers.html
DIE GLEICHUNG DER POPULATIONSDICHTE : D=c/d =c/(2pm).
Die Dichte D hängt allein vom äquidistanten Intervall d der Zahlenelementen unterschiedlicher
Periodenbahnen ab. Die Konstante c bezeichnet die Anzahl von Bahnelementen ( es sind immer
2), die an beiden Enden der d-Variablen unmittelbar gegenüber liegen. Die Hyperbelgleichung
sagt aus: die Dichte D von Primzahlen pm hat einen dem Nullwert zustrebenden endlichen Verlauf.
Es gibt also, wegen der Konvergenz, eine asymptotisch endliche Primzahlen-Population. Demnach
negiert die Dichtegleichung die 4. Prim-Kardinalfrage: Existiert unendlich viele Primzahlen
?.
DIE AFFIRMATION DER UNENDLICHKEITSFRAGE DURCH EUKLID UND EULER
Euklids Lösungsansatz zur Frage nach der Gesamtmenge der Primzahlen war die Anwendung
des Syllogismus-Diskurses auf Primzahlen. http://aleph0.clarku.edu/~djoyce/java/elements/bookIX/propIX20.html.Eulers
Ausgangspunkt war die Divergenz-Eigenschaft der Harmonischen Reihe angewandt auf reziproken
Primzahlen: Sp=1/2 +1/3 + 1/5 + 1/7..... Beide Wege führten zur Affirmation der Unendlichkeit
von Primzahlen. Einen weiteren Lösungsweg bietet heute Digital-Database bestehend aus
Primfaktoren (also nicht aus der Liste von bekannten Einzelprimzahlen), Die uns heute leicht
zugänglichen Primfaktoren standen bis zum Ende des 2. Jahrtausends nach Euklid mangels
des mit fast Lichtgeschwindigkeit laufenden Digitalrechners nicht hinreichend zur Verfügung.
Wir werfen einen Blick auf das Umfeld der Primforschung von damals und heute: Um, zum Beispiel,
die Verteilung von großen Primzahlen verfolgen zu können, müssen Primfaktoren
von Zahlen auch in dieser Größenordnung erreichbar sein: N= 1234567890123456= 26
x 72 x 3013191 x 13065091. (Ausführungszeit 18719 Millisekunden.). Das aber stellt eine
Aufgabe dar, die ohne Frage mit der Abakus-Technologie in den Zeitaltern von Euklid und Euler
ebenso sowenig zu bewältigen war, wie die Aufgabe, die Voraussage des Atoms von Demokrits
(460-370 BC) vor der Erfindung des Reagenzglases experimentell nachzuweisen.
Die Primfaktoren-Gleichung und Umwandlung N = pm x p1a x p2b x p3c x = pm(2n+1) entstehen unmittelbar
aus derartiger Primfaktoren-Database q= pm x p1a x p2b x p3c x, die aus beliebigen Segmenten
laufender natürlicher Zahlen errechnet wurden. Segmente laufender natürlicher Zahlen
haben sich als sine qua non erwiesen, um eine Gegenüberstellung von der natürlichen
Zahl N und den Primfaktoren q vor Ort zu verfolgen,
was auch schließlich zum Aufspüren der lang gesuchten Verbindung „missing link“
zwischen N und ihren Bausteinen q geführt hat.
Und nun zurück zum Unendlichkeitsproblem. Man erkennt, dass die Dichtegleichung D=c/(2pm).
, die die Unendlichkeit negiert , aus demselben Hauptsatz der elementaren Zahlentheorie entsteht
- N = pm x p1a x p2b x p3c x = pm(2n+1) mit .(. p < p1 < p2 < p3..... alle Primzahlen
) - wie die verifizierbare neu vorgestellte mathematische Definition der Einzelprimzahl: m=1
und n=0 . Im Gegensatz dazu: Es fehlt eine ableitbare Verbindung zwischen der traditionellen
Definition „ Eine Primzahl lässt sich nur durch sich selbst und die Zahl 1 teilen“,
die sich nicht in mathematischer Gleichung erfassten lässt, und der Affirmation der Primzahlfrage.
(Details über Primfaktoren-Database mit Hinweis auf N/q-Beziehungen sind erhältlich
bei: kkudiabor@computeriq-research.net
)
.UNENDLICHE ELEMENTE AUS ENDLICHEN BAUSTEINEN
Aus einer endlichen Population von Primzahlen unendliche natürliche Zahlen zu generieren
stellt auch hier in diesem Falle kein einzigartiges Phänomen in der natur dar. Häufig
kann man das Prinzip beobachten, nach welchem aus endlicher Anzahl von Bausteinen unendlich
viele Elemente hervorgehen. So besteht die gesamte Materie des unendlichen Universums aus den
94 natürlich vorkommenden Atomen. Und der Bauplan des Lebens mit all seinem Evolutionsvielfach
und unendlicher Fibonacci-Reproduzierbarkeit lässt sich auf nur 4 DNA-Bausteinen zurückführen:
Adenine, Thymine, Guanine und Cytosine Man kann das hier wirkende Prinzip E paucis plures beschreiben.
DAS EINHEITSPRINZIP DER PRIM- UND ATOM PERIODENSYSTEME:
Np =pm(2n+1); Na=21(2n+1)
Aus der Gegenüberstellung A) und B) unten geht hervor, dass sich die Gleichung der Grundstruktur,
s p d f, des Atom-Periodensystems in B) unmittelbar aus der Gleichung des Prim-Periodensystems
in A) ableitet. In der Dreieck-Präsentation besteht s p d f aus dem Segment von den 4
obersten Elementen auf der 21-Periodenbahn: N={2,6,10,14}.={21x1, 21x3, 21x5, 21x7} .
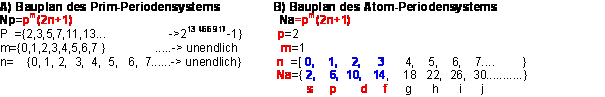
Offenbar braucht die Natur nicht mehr als die 4 Elemente, um die Gleichung des Aufbauprinzips
der 94 natürlich vorkommenden Elemente der Materie aufzustellen. Man beachte: Die Wurzeln
der Übertrageinheiten des Dezimal- und Dualsystems sind konstant: 10n bzw. 2n Dagegen
sind sie bei Modular-Arithmetik (clock arithmetic) variable: : 601[sek.], 601[min.], 241[Std.]
71[Tage]. Man stellt fest: die Übertrageinheiten des s p d f -Systems ist auch modular::
nS21, np61, nd101, nf141: Und Gleiches gilt auch für die Übertragachse von Prim-Exponenten
in dem Dreieck-Periodensystem: pm ={22, 23, 32, 24, 52, 33,25, 72, 26, 34...}. Die Frage drängt
sich auf: inwiefern kann man die 94 Ordnungszahlen des Mendelejeff- Periodensystems aus zahlentheoretischen
Gesetzmäßigkeiten des Prim-Periodensystems entwickeln, die das physikalisch chemische
Verhalten wie die Hundsche Regel oder Anomalien wie die Cr-Konfiguration [Ar]3d54s1 studieren
lassen. Solche Gedanken erhalten ihre Legitimität durch den gemeinsamen Ursprung beider
Periodensysteme Np und Na, und vor allen Dingen durch den Drang der Natur zur Einfachheit,
die in Np und Na so eindrucksvoll manifestiert wird,
Die Natur ist einfach und schwelgt nicht
in überflüssigen Ursachen der Dinge (Issac Newton:)
Bei Fragen, Anregungen, Vorschlägen, Kritiken und schicken Sie bitte mir eine E-Mail (webmaster@primzahlen.de)